Makine öğrenimi için gerekli algoritma becerileri nasıl elde edilir? | Teknik Başlıklar
Bu makale, yaygın olarak kullanılan üç makine öğrenimi optimizasyon algoritmasını (Newton yöntemi, gradyan iniş yöntemi ve en dik iniş yöntemi) tanıtıyor ve karşılaştırıyor ve optimizasyon algoritmalarının seçimi hakkında bazı öneriler vermek için algoritmanın matematiksel ilkelerini ve gerçek durumları birleştiriyor.

Yazar | Nasir Hemed
Derleme | Rachel
Üretildi | AI Technology Base Camp (id: rgznai100)
Temel hazırlık
- Lineer Cebir
- Çok Değişkenli Kalkülüs
- Konveks fonksiyonların temel bilgisi
Hepimiz makine öğrenimindeki en önemli içeriklerden birinin optimizasyon olduğunu biliyoruz. Bu nedenle, işlevi makul şekilde optimize edebilecek bir algoritma bulmak her zaman bizim için önemlidir. Şu anda en çok kullandığımız optimizasyon algoritmalarından biri de gradyan iniş algoritmasıdır. Bu yazıda, gradyan iniş algoritmasını ve diğer bazı optimizasyon algoritmalarını tanıtacağız ve bunları teorik bir perspektiften anlamaya çalışacağız. Bu makalede tanıtılan temel algoritmalar şunları içerir:
- Newton Yöntemi (Newton Yöntemi)
- Dik iniş
- Dereceli alçalma
Bu algoritmalar hakkında daha fazla bilgi edinmek istiyorsanız, Stanford Üniversitesi'nin "Konveks Fonksiyon Optimizasyonu - Üçüncü Bölüm" ders kitabını okuyabilirsiniz. Bu yazıda, esas olarak ikinci dereceden fonksiyonlara ve polinom fonksiyonlarına odaklanıyoruz.
Optimizasyon fonksiyonları için temel varsayımlar
Genel olarak, uğraştığımız fonksiyonların türevlerinin sürekli olduğunu varsayıyoruz (örneğin, f C¹). Newton yöntemi için, fonksiyonun ikinci türevinin de sürekli olduğunu varsaymamız gerekir (örneğin, f C²). Son olarak, küçültülecek fonksiyonun dışbükey olduğunu da varsaymalıyız. Bu şekilde, algoritmamız bir noktaya yoğunlaşırsa (genellikle yerel minimum denir), bu değerin küresel bir optimum olduğunu garanti edebiliriz.
Newton Yöntemi
- Tek değişkenli fonksiyonlar durumu
Newton yönteminin temel fikri, optimize edilmesi gereken f fonksiyonunun yaklaşık olarak yerel olarak ikinci dereceden bir fonksiyon olarak ifade edilebileceğidir. Bu ikinci dereceden fonksiyonun sadece minimum değerini bulmamız ve bu noktada x değerini kaydetmemiz gerekiyor. Minimum değer artık değişmeyene kadar bu adımı daha sonra tekrarlayın.
- Çok değişkenli fonksiyonlar durumu
Tek değişkenli durumlar için, Newton'un yöntemi daha güvenilirdir. Ancak gerçek problemlerde, çok az sayıda tek değişkenli durumla uğraşıyoruz. Çoğu zaman, optimize etmemiz gereken fonksiyon birçok değişken içerir (örneğin, n gerçek sayılar kümesinde tanımlanan fonksiyon). Bu nedenle, burada çok değişkenli durumu tartışmamız gerekiyor.
X n varsayarsak, o zaman:
x_n = başlangıç_ noktası x_n1 = x_n-ters (hessian_matrix) (gradyan (x_n)) iken (f (x_n)! = f (x_n1)): x_n = x_n1 x_n1 = x_n-ters (hessian_matrix) (gradyan (x_n))
Bunlar arasında, gradyan (x_n), fonksiyon x_n noktasında olduğunda gradyan vektörüdür, hessian_matrix, nxn boyutunda bir Hessian matrisidir ve değeri, x_n'deki fonksiyonun ikinci türevidir. Matris dönüşümünün algoritma karmaşıklığının çok yüksek olduğunu hepimiz biliyoruz ( O (n³) ), bu nedenle Newton yöntemi bu durumda yaygın olarak kullanılmamaktadır.
Dereceli alçalma
Gradyan inişi, makine öğrenimi ve diğer optimizasyon problemlerinde açık ara en çok kullanılan optimizasyon algoritmasıdır. Gradyan algoritmasının temel fikri, her yinelemede gradyan yönünde küçük bir adım atmaktır. Gradyan algoritması ayrıca her adımın adım uzunluğunu belirten sabit bir alfa değişkeni içerir. Aşağıda algoritmanın bir örneği verilmiştir:
alpha = small_constantx_n = başlangıç_pointx_n1 = x_n-alpha * gradient (x_n) while (f (x_n)! = f (x_n1)): # x_n = x_n1 x_n1 = x_n-alpha * gradient (x_n) yakınsaması uzun zaman alabilirBurada alfa, her yinelemede x_n güncellenirken kullanılması gereken bir değişkendir (genellikle hiperparametre olarak adlandırılır). Aşağıda alfa değerinin seçimi hakkında basit bir analiz yapıyoruz.
Büyük bir alfa seçersek, muhtemelen en iyi noktayı geçer ve en iyi noktadan gitgide uzaklaşırız. Aslında, alfa değeri çok büyükse, en iyi noktadan bile tamamen sapacağız.

Alfa değeri çok büyük olduğunda, 10 yinelemeden sonra gradyan azalır
Ek olarak, seçtiğimiz alfa değeri çok küçükse, optimum değeri bulmak için birçok yineleme gerekebilir. Ve optimal değere yakın olduğumuzda, gradyan sıfıra yakın olacaktır. Bu nedenle, alfa değeri çok küçükse, asla en iyi noktaya ulaşamayabiliriz.

Alfa değeri çok küçük olduğunda, 10 yinelemeden sonra gradyan azalır
Bu nedenle, en iyi seçeneği bulmak için daha fazla alfa değeri denememiz gerekebilir. Uygun bir alfa değeri seçersek, yinelemede genellikle çok zaman kazanabiliriz.

Alfa değeri makul olduğunda, gradyan 10 yinelemeden sonra azalır
En dik iniş yöntemi
En dik iniş yöntemi, gradyan iniş yöntemine çok benzer, ancak en dik iniş yöntemi, her yineleme için en uygun adım boyutu değerini gerektirir. Aşağıda, en dik iniş yönteminin algoritmasına bir örnek verilmiştir:
x_n = başlangıç_pointalpha_k = get_optimizer (f (x_n-alpha * gradyan (x_n))) x_n1 = x_n-alpha_n * gradyan (x_n) iken (f (x_n)! = f (x_n1)): x_n = x_n1 alpha_k = get_optimizer (f (x_n-alpha * gradyan (x_n))) x_n1 = x_n-alpha_n * gradyan (x_n)
Bunlar arasında, x_n ve x_n1, algoritmanın girdisi olan n üzerindeki vektörlerdir, gradyan f fonksiyonunun x_n noktasındaki gradyanıdır ve alpha_k'nın matematiksel ifadesi aşağıdaki gibidir:

Bu nedenle, orijinal işlevi optimize ederken, her yinelemede bir dahili işlevi optimize etmemiz gerekir. Bunun avantajı, bu dahili optimizasyon fonksiyonunun tek değişkenli bir fonksiyon olması ve optimizasyonunun çok karmaşık olmayacak olmasıdır (örneğin, burada fonksiyon olarak Newton metodunu kullanabiliriz). Ancak daha fazla durumda, bu işlevi her adımda optimize etmek daha pahalı maliyetler getirecektir.
- İkinci dereceden fonksiyonların özel durumları
Ortalama kare hata fonksiyonu için:
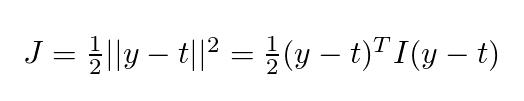
onların arasında, ben Kimlik matrisi mi, y = Qw + b . Tartışmayı basitleştirmek için, burada sadece w ağırlığının optimal değerini bulma durumunu ele alıyoruz (b'nin sürekli olduğunu varsayarak). Denklemi koy y = Qw + b Yukarıdaki formülü getirip biraz sıralama yaptıktan sonra aşağıdaki denklemi elde edebiliriz:

Şimdi tekrar kontrol edelim g () , Puan kullanırsak bulacağız k Optimal değer olduğu için gradyan sıfır olmalıdır. Yani aşağıdaki denklemimiz var:

Yukarıdaki formülü basitleştirin ve değiştirin f Gradyanını getirdikten sonra, alabiliriz k Temsil aşağıdaki gibidir:

Bu, ikinci dereceden fonksiyonlar durumunda k Değer.
- İkinci dereceden fonksiyonun yakınsama analizi
İçindeki tanım için ² Yukarıdaki ikinci dereceden fonksiyon, en dik iniş yöntemi genellikle optimum değere çok yakın olduğunda ve kullanılan adımların sayısı on adımı geçmediğinde kullanılır.

4 yinelemeden sonra 2D'de en hızlı iniş
Yukarıdaki şekilde, her yinelemedeki değişimin yönü dikeydir. 3 ila 4 yinelemeden sonra, türevdeki değişimin temelde ihmal edilebilir olduğunu görebiliriz.
- Neden en dik iniş yöntemi nadiren kullanılır?
En dik iniş algoritması, hiperparametre ayarlama ihtiyaçlarını karşılar ve yerel minimumun bulunabilmesini sağlar. Peki bu algoritma neden pek kullanılmıyor? En dik iniş yöntemiyle ilgili sorun, her adımın nispeten pahalı olan aplha_k'yı optimize etmesi gerektiğidir.
Örneğin, ikinci dereceden fonksiyonlar için, her yineleme, birden çok matris çarpımı ve vektör nokta çarpımı gerektirir. Ancak gradyan iniş için, sadece türevi hesaplamanız ve her adımda değeri güncellemeniz gerekir.Bunu yapmanın maliyeti, en dik iniş algoritmasından çok daha düşüktür.
En dik iniş algoritmasının bir başka sorunu, dışbükey olmayan fonksiyonları optimize etmenin zor olmasıdır. Dışbükey olmayan işlevler için aplha_k sabit bir değere sahip olmayabilir.
Gradyan iniş yöntemi ile en dik iniş yönteminin karşılaştırılması
Bu bölümde gradyan iniş yöntemi ile en dik iniş yöntemini karşılaştırıyor ve zaman maliyetindeki farklarını karşılaştırıyoruz. İlk olarak, iki algoritmanın zaman maliyetini karşılaştırdık. İkinci dereceden bir fonksiyon oluşturacağız: f: ² (Fonksiyon bir 2000x2000 matristir). Bu işlevi optimize edeceğiz ve yineleme sayısını 1000 ile sınırlayacağız. Bundan sonra, iki algoritmanın zaman maliyetini karşılaştıracağız ve x_n değeri ile en iyi nokta arasındaki mesafeyi kontrol edeceğiz.
Önce en dik iniş yöntemine bakalım:
0 Diff: 117727672.56583363 alpha değeri: 8.032725864804974e-06100 Diff: 9264.791000127792 alpha değeri: 1.0176428564615889e-05200 Diff: 1641.154644548893 alpha değeri: 1.0236993350903281e-05300 Diff: 590140a : 1.0263893422517941e-05500 Diff: 155.43169915676117 alpha değeri: 1.0270028681773919e-05600 Diff: 96.61812579631805 alpha değeri: 1.0274280663010468e-05700 Diff: 64.8465923780449 alpha değeri: 1.027728586 Fark: 34.00975978374481 alfa değeri: 1.0281092917213468e-05 Optimizer, x = ve f (x) = - 511573479.5792374 ile 1000 yinelemede bulundu Alınan toplam süre: 1 dakika 28snAşağıdakiler, alfa = 0,000001 olan gradyan iniş yöntemidir:
0 Diff: 26206321.312622845 alpha değeri: 1e-06100 Diff: 112613.38076114655 alpha değeri: 1e-06200 Diff: 21639.659786581993 alpha değeri: 1e-06300 Diff: 7891.810685873032 alpha değeri: 1e-06400 Diff: 3793.909e6611500 Diff: 2143.767760157585 alpha değeri: 1e-06600 Diff: 1348.4947955012321 alpha değeri: 1e-06700 Diff: 914.9099299907684 alpha değeri: 1e-06800 Diff: 655.9336211681366 alpha değeri: 1e-06900 Diff: 490.0588a değeri: 1e-0667 X = ve f (x) = - 511336392.26658595 ile 1000 yinelemede bulundu Alınan toplam süre: 1dk 16snGradyan iniş yönteminin hızının en dik iniş yönteminden biraz daha hızlı olduğunu (birkaç saniye veya dakika) bulabiliriz. Ancak daha da önemlisi, en dik iniş yönteminin benimsediği adım boyutu, gradyan iniş yönteminden daha mantıklıdır, ancak gradyan iniş yönteminin değeri optimal değildir. Yukarıdaki örnekte, gradyan iniş algoritması için, f (xprex) ile f (akım) 900. yinelemedeki fark 450'dir. En dik iniş yöntemi, daha önce birçok yinelemeyle bu değere ulaşmıştır (yaklaşık olarak 300. ve 400. yinelemeler arasında).
Bu nedenle, en dik iniş yönteminin yineleme sayısını 300 ile sınırlandırmaya çalışıyoruz ve çıktı aşağıdaki gibi:
0 Diff: 118618752.30065191 alpha değeri: 8.569151292666038e-06100 Diff: 8281.239207088947 alpha değeri: 1.1021416896567156e-05200 Diff: 1463.1741587519646 alpha değeri: 1.1087402059869253e-05.1993 Diff: 1.1087402059869253e-05.1993 f (x) = - 511526291.3367646, 400 yinelemede Alınan süre: 35.8snEn dik iniş yönteminin hızının aslında daha hızlı olduğu görülebilir. Bu durumda, optimum değere her yinelemede daha az adımla yaklaşabiliriz. Aslında, amacınız optimum değeri tahmin etmekse, en dik iniş yöntemi gradyan iniş yönteminden daha uygundur. Düşük boyutlu fonksiyonlar için, 10 adımlı en dik iniş yöntemi, 1000 iterasyondan sonra gradyan iniş yöntemine göre optimum değere daha yakın olacaktır.
Aşağıdaki örnekte, bir tanım kullanıyoruz ³ İkinci dereceden fonksiyon hakkında. 10 adımdan sonra en dik iniş yöntemiyle elde edilen fonksiyon değeri f (x) = -62434.18'dir. 1000 adımdan sonra gradyan iniş yöntemi ile elde edilen fonksiyon değeri f (x) = -61596.84'tür. 10 adımdan sonra en dik iniş yönteminin sonucunun 1000 adımdan sonra gradyan iniş yönteminin sonucundan daha iyi olduğu görülebilir.
Bu durumun yalnızca ikinci dereceden işlevlerle uğraşırken geçerli olduğunu unutmayın. Genel olarak, her yinelemede en uygun k değerini bulmak daha zordur. G () fonksiyonunun optimal değerini bulmak her zaman k'nin optimal değerini elde etmez. Optimizasyon işlevini en aza indirmek için genellikle yinelemeli bir algoritma kullanırız. Bu durumda en dik iniş yöntemi gradyan iniş yöntemine göre daha yavaştır. Bu nedenle, en dik iniş yöntemi pratik uygulamalarda yaygın değildir.
sonuç olarak
Bu yazıda üç iniş algoritması öğrendik:
- Newton yöntemi
Newton yöntemi, işleve ikinci dereceden bir yaklaşım sağlar ve işlevi her adımda optimize eder. En büyük sorun, çok değişkenli durumlar için (özellikle birçok vektör özelliği olduğunda) çok pahalı olan optimizasyon sürecinde matris dönüşümünün gerekli olmasıdır.
- Dereceli alçalma
Gradyan inişi, en yaygın kullanılan optimizasyon algoritmasıdır. Algoritma her adımda sadece türevi hesapladığı için maliyeti daha düşük ve hızı daha hızlıdır. Bununla birlikte, bu algoritmayı kullanırken, adım uzunluğunun hiperparametreleri üzerinde çok sayıda tahmin ve girişimde bulunmak gerekir.
- En Dik İniş
En dik iniş yöntemi, her adımda fonksiyonun gradyan vektörü için optimum adım uzunluğunu bulur. Sorun, ilgili işlevlerin her yinelemede optimize edilmesi gerektiğidir ve bu da çok fazla maliyet getirecektir. İkinci dereceden fonksiyonlar söz konusu olduğunda, her adım çok sayıda matris işlemi içerse de, en dik iniş yönteminin etkisi yine de daha iyidir.
İlgili notlar için lütfen şunlara bakın:
https://colab.research.google.com/gist/nasirhemed/0026e5e6994d546b4debed8f1ed543c0/a-deeper-look-into-descent-algorithms.ipynb
Orijinal bağlantı:
https://towardsdatascience.com/a-deeper-look-at-descent-algorithms-13340b82db49
-

- Merkez Maliye ve Ekonomi Komitesi fiyat durumundan bahsetti: Para politikası enflasyonu nasıl gözlemliyor?
-

- Kadın otomobil sahibini savunan Mercedes-Benz haklarını tahsil etmekle suçlandı Avukat: müşteri "koşmuyor"