Dünya topolojide farklı

Resim kaynağı: Pixabay
yazı
Lin Kailiang (Matematik Doktorası, Capital Normal Üniversitesi, şu anda Northwest A&F Üniversitesi Fen Fakültesi'nde öğretim üyeliği yapıyor)
Geçen yılki Nobel Fizik ve Kimya Ödülü'nün her ikisi de topolojinin harika uygulamalarından bahsetti ve ondan sonra, birkaç kez topolojiyi matematiksel çevrenin dışındaki meraklı arkadaşlarım arasında popülerleştirmem istendi. Ne yazık ki uygun bir giriş noktası bulamamıştım. Daha yeni, durumu açmadan önce yüksek matematik dersinde yaptığım bir şakayı düşündüm. Önce bu şakayı gözden geçireyim.
9 Ekim 2014, bir ay boyunca podyuma çıktığım (matematik dersi verdiğim) gündü. Dersten sonra blogda bir yorum yaptım:
Bugünün içeriği, işlevin eşitsizliğidir. Kalemi elime aldığımda, içbükey ve dışbükey iki karakterin vuruş sırası konusunda tamamen anlaşılmaz olduğumu fark ettim ... Utanç, bir ilkokul öğrencisi bile, ama bir üniversite öğretmenim kayıplara uğramıştı. Baştan savma geçmesine rağmen, ama iyi bir örnek oluşturmadım ...
O zamanlar utandığımı hatırlıyorum ve yurtdışında okuyan birçok öğrencinin iş bulmak için Çin'e dönme konusunda isteksiz olmasının sebebinin "çarpma" kelimesini yazmaktan korkmaları olduğunu düşündüğüm için hala şaka yaptım. Arkadaşlarımın ara sıra yaptığı yorumlarda, cebirsel geometri konusunda uzmanlaşmış bir geri dönen kişinin yorumunu gördüm: "İki kelimeyi iki vuruşta içbükey ve dışbükey yazabilirim ..."
O zamanlar, hala "çarpma" nın neden olduğu hayal kırıklığı içinde sıkışıp kaldım. Sözlerinin bir anlam ifade ettiğini düşünmedim. Bugün aniden haklı olduğunu fark ettim! Matematikçilerin bakış açısından (özellikle topologlar ve grafik teorisyenleri), iki kelime içbükey ve dışbükey "tek vuruşta boyanabilir". Yani genel bir sorumuz var: topoloji perspektifinden, herhangi bir Çince karakteri çizmek için en azından kaç vuruşa ihtiyacımız var? Kolaylık sağlamak için, buna Çince karakterlerin "topolojik vuruş sayısı" diyoruz.
Genel sonuçları tanıtmadan önce birkaç örneğe bakalım.
İçbükeylik ve dışbükeylik elbette "tek vuruş" olabilir ve ağızlar da öyle. Daha basit örnekler Yi, B, Ji, Si, Ji, Gong, Le ve Factory'dir. Biraz daha az belirgin olanlar Zhong, Chuan, Ri ve Yue'dur. . İki toplam iki vuruş gerektirir, yani "topolojik vuruşları" her ikisi de 2'dir. Mewada'nın "topolojik vuruşları" da 2'dir. Buradan, genel olarak konuşursak, bir Çince karakterin "topolojik vuruş sayısı" nın, genellikle yazdığımız vuruş sayısından daha az olduğu görülebilir. Elbette tamamen aynı olan durumlar da var mesela sınıftaki halk seçimlerinde yaygın olarak kullanılan imla karakterlerinin vuruş sayısı 5, "topolojik vuruş" sayısı hala 5.
Çince karakterlerle sınırlı olmayıp, harflerin ve sayıların "topolojik vuruş sayısını" da inceleyebiliriz. Örneğin, 8 rakamı ve onun dökümünü "topolojik vuruşları" ile aynı olan B harfinin "topolojik vuruşlarını" (kaç tane?) Sayabilirsiniz!
Daha genel olarak, bir ağın (bir şehrin otobüs güzergah ağı gibi) "topolojik vuruşlarını" sayabiliriz (bu, tüm ağı kapsayacak şekilde en az otobüs güzergahının düzenlenmesine karşılık gelir). Matematiksel açıdan bu son derece ilginç bir sorudur. Çince karakterler sorusuna dönersek bile, basitliği savunan hattatlar, bir Çince karakterin "topolojik vuruşlarının" ne olduğunu bilmekten mutlu olabilirler.

2007'de Chengdu otobüs ağının şematik diyagramı
Matematik açısından bir Çince karakter bir grafik olarak kabul edilebilir. Bir grafik, birkaç (genellikle sonlu sayıda) köşeden oluşan bir koleksiyondur ve bu köşeler arasında bazı bağlantı ilişkileri (bağlantı çizgileriyle gösterilir) belirtilmiştir. Bu nedenle bir grafik, yapısı olan bir dizi noktadan (yani bağlantılı ilişkileri temsil eden kenarlardan) başka bir şey değildir.
Çince bir karakteri grafik olarak ele almak için, sadece uç noktaları, her bir konturun bükülme noktalarını ve herhangi iki çizginin kesişme noktalarını köşe olarak işaretlememiz gerekir. Bu anlamda dışında hemen hemen her Çince karakter bir resimdir.
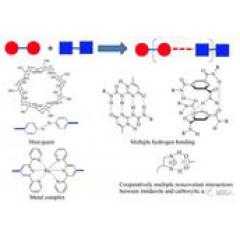
Matematiksel terim resmi ilk olarak 1878'de İngiliz matematikçi J. J. Sylvester tarafından tanıtıldı. O sırada düşündüğü şey, moleküllerin yapısını tanımlamak için diyagram kavramını kimyaya uygulamaktı. Örneğin, metan CH4 molekülünün resminin normal bir tetrahedron olduğunu, dört hidrojen atomunun H normal tetrahedronun dört köşesinde yer aldığını ve C karbon atomunun merkezde olduğunu ve kimyasal bağlarla her hidrojen atomuna bağlı olduğunu hepimiz biliyoruz.
Bilgisayar bilimiyle ilgili ağ ve hatta sıradan kişiler arası ağ da bir tür grafik olarak kabul edilebilir. Örneğin, aslında bir grafik teorisi olan "altı derece bölütleme teorisi" ni duymuş olabilirsiniz. Tahmin edebileceğiniz gibi, grafik teorisinin birçok uygulaması vardır.
Grafiklerin incelenmesi bir bilim, yani grafik teorisi oluşturdu. Grafik teorisinin araştırması, 1736'da büyük İsviçreli matematikçi Euler'in çalışması olan bir grafiğin "topolojik vuruş sayısını" belirleme probleminden başladı. Bu nedenle, Euler grafik teorisinin kurucusu olarak kabul edilir ve 1736, "grafik teorisinin ilk yılı" olarak adlandırılabilir.
Euler tarafından çözülen grafik teorisi problemi daha sonra "Königsberg'in Yedi Köprüsü" olarak biliniyordu. Soyutlamadan sonra soru şudur: Aşağıdaki ağ "tek vuruşlu" olabilir mi; "tek vuruşlu" olamazsa, kaç "topolojik vuruş" nedir? (Okuyucular önce denemek isteyebilir.)

Königsberg'in yedi köprüsünün resmi
Eulerin harika sonuçlarını bildirmeden önce, bu sorudaki "topoloji" nin nerede göründüğünü açıklamaya odaklanmak istiyorum. Aslında topoloji, arkadaşımın yorumunda en başından beri ortaya çıktı. "İki karakteri" içbükey ve dışbükey "iki vuruşta yazabilirim" dediğinde aslında gizli bir anlam vardır, yani içbükeylik ve dışbükeylik "eşbiçimli" dir (aynı yapı).
İki Çince karakterin (daha genel, iki grafiğin) izomorfik olduğunu söylüyoruz, bu da köşe kümeleri arasında bire bir yazışma olduğu anlamına gelir, böylece ilk Çince karakterin köşeleri arasındaki bağlantı ilişkisi bu yazışma altında değişmeden kalır. değişiklik.
Kimyaya karşılık olarak, aynı bileşime (köşe) sahip iki bileşik farklı konfigürasyonlara sahipse (bağlantı ilişkisi eşleşemez), bunlar birbirlerinin izomerleri olarak adlandırılır.
İçbükey ve dışbükey durumunda, bunların izomorfizmi açıktır.
Topolojik bir bakış açısıyla, Çince karakterleri incelediğimizde, aynı yapıdaki karakterleri eşdeğer olarak görebiliriz. Bu nedenle, topologların görüşüne göre içbükey ve dışbükey aynıdır. Şimdi lütfen şu üç soruyu düşünün: Sol ve sağ eşbiçimli midir, güneş ve ay eşbiçimli midir ve gökyüzü ile yer eşbiçimli midir?
Sezgi size bu üç sorunun cevabının hayır olduğunu söyleyecektir. Bu soruları son derece kesin bir şekilde cevaplamak istiyorsanız, bazı temel gözlemlere ihtiyaç vardır.
İlk gözlem, iki Çince karakter aynı yapıya sahipse, köşe sayısının aynı olması gerektiğidir. Bunun nedeni, izomorfizmin iki Çince karakterin köşe kümeleri arasında bire bir yazışmayı gerektirmesidir. Şimdi bu kelimelerin köşelerini sayarsanız, yapı olarak doğal olarak farklı olan solda 11 ve sağda 9 köşe olduğunu göreceksiniz. Benzer şekilde, güneş ve ay, gökyüzü ve yeryüzü farklı yapıdadır.
Gökyüzünün ve yeryüzünün farklı yapısı bir bakışta bile görülebiliyor: çünkü yeryüzü sağ-sol bir yapı olduğu için iki bağımsız parçaya (toprak ve yeryüzü) ayrılıyor.
Matematiksel olarak konuşursak, Çince bir karakterin "blok sayısı" na bağlı bileşenlerin sayısı denir. Sözde "bloklar" bağlantılı parçalardır (bağlı dallar). Örneğin, ağza bağlı bileşenlerin sayısı elbette 1 iken, Lu ve Pin'in bağlı bileşenlerinin sayısı sırasıyla 2, 3'tür. Gök ve yerin birbirine bağlı dallarının sayısı sırasıyla 1 ve 2'dir. Grafik teorisi veya topoloji perspektifinden, gökyüzü ile yeryüzü (veya toprak) arasındaki bağlı dalların sayısındaki fark, gerçek "dünya farkı" dır. "Dünya topolojide farklıdır", işte nedeni budur. Benzer şekilde, "Ding Ding'dir ve Mao Mao'dur" sözü de topoloji perspektifinden anlaşılabilir.Ding ile Mao arasındaki fark ilk olarak bağlı bileşenlerin sayısına yansır.
Aynı yapıya sahip Çince karakterlerin aynı sayıda bağlı bileşene sahip olduğunu görmek kolaydır. Jargonda, bağlı bileşenlerin sayısı izomorfik değişmezdir. Buradan yine (daha basit bir şekilde) cennetin ve dünyanın yapılandırılmadığını yargılayabiliriz.
Bu örnek bize, iki Çince karakterin izomorfik olup olmadığını belirlerken, yukarıda bahsedilen bağlı bileşenlerin sayısı gibi bazı izomorfik değişmezleri kavramanın yararlı olduğunu söyler. Matematiğin önemli bir amacı, bazı nesnelerin izomorfizm anlamında sınıflandırılmasını sağlamaktır.Önemli bir yöntem de izomorfik değişmezleri bulmaktır. Geçen yıl Nobel Fizik Ödülünde bahsedilen Chern sayısı (aynı isimli kadın film yıldızı değil), ünlü matematikçi Chern tarafından keşfedilen son derece önemli bir topolojik değişmezliktir.
Çince bir karakterin bağlı bileşen sayısı 1 ise, Çince karakterin bağlı olduğunu söyleriz. Açıkçası, tek vuruşta çizilebilen Çince karakterler birleştirilmelidir. Bunun tersi doğru değildir: Tian, Yue, Ji, Mu, Tian, Jia, Shen ve Mu gibi bağlı bir Çince karakter (ağ) tek vuruşta çekilemez olabilir. Başka bir deyişle, bağlı bileşenlerin sayısı tamamen izomorfik bir değişmez değildir. Bu, biraz daha karmaşık izomorfik değişmezler olduğu anlamına gelir. Daha önce bahsettiğimiz "topolojik vuruş sayısı" nın da izomorfik değişmez olduğunu bulmak zor değildir: Aynı yapının Çince karakterleri (veya resimleri) aynı "topolojik vuruş sayısına" sahip olmalıdır. Elbette, bağlı bileşenlerin sayısı kadar kullanışlı değildir, çünkü Çince bir karakterin "blok sayısı" nın sayılması genellikle bir bakışta bilinir.
Topoloji (ve belki de hattatlar) perspektifinden bakıldığında, en basit Çince karakterler sadece bir vuruştur. Tüm Çince karakterleri izomorfik ilişkiye göre sınıflandırmayı düşünmeyeceğiz (bu soru biraz sıkıcı görünüyor), ancak yalnızca tek vuruşta çizilebilecek tüm Çince karakterleri sınıflandırmayı düşüneceğiz.
Prensip olarak, en yaygın olan ağız, içbükey, dışbükey, B, Ji, Si, Ji, Çince, Japonca, Japonca hariç, tek vuruşta çizilebilecek çok fazla Çince karakter yoktur (sorun yaşamamak için geçici olarak hariç tutuyoruz) Chuan, Gong, Le ve Factory, matematiği öğrenenlere tanıtmaya değer başka bir kelime daha var, yani Zhe Bu kelime güç için arkaik bir kelime olan "Mi" olarak telaffuz edilir. Konuyu başka yöne çevirip kelimeyi biraz açıklayayım. Matematik tarihçisi Bay Liang Zongju'nun "Gücün ve Üslü Kavramların Gelişimi ve Sembollerin Kullanımı" adlı makalesinden öğrendim:
"Men" kelimesi, yiyecekleri havluyla örtmek için bir isim olarak kullanılır; bir fiil olarak havluyla örtmek için kullanılır. "Shuowen Jiezi" şöyle açıklanıyor: "Zhe, Fu Ye, aşağıdan aşağı." Ve "Yu Pian": "Zhe, her şeyi havluyla ört."
Eşyaları kare bir bezle örtün ve bir zhe şekli oluşturmak için dört köşesinden asın. Bu anlamı genişleterek, kare olan her şeye güç de denebilir. Daha da genişletmek için, bir dikdörtgenin alanı veya iki sayının çarpımı (özellikle bir sayının kendisiyle çarpılmasının sonucu) da kuvvet olarak adlandırılır. Mevcut literatüre bakılırsa, bu promosyon Liu Hui ile başladı ...
Bay Liang, matematikte iktidar teriminin uygulanışını göstermek için makaleye birçok örnek ekledi. Sadece iki nokta ekliyorum:
Birincisi, ortaokul matematiğinde bir nokta teoreminin gücü, gücün ortaya çıkmasının nedeni, içinde bir ürün olmasıdır.
İkincisi, Yang Mi'nin neden Yang Mi olarak adlandırıldığını şimdi tahmin edebilmelisiniz, çünkü ebeveynlerinin her ikisi de Yang soyadındadır ve ortak adı Yang Pingfang olmalıdır! (Tahmin edebileceğiniz gibi, ona isim veren kişi matematik konusunda çok iyi eğitilmiş!) Baidu yazısında şöyle dedi: "Üç kişilik bir ailenin adı" Yang "ın üçüncü gücü olan Yang, bu yüzden ona Yang Mi adını verdim. Girişin yazarı iyi anlamamış olabilir: Yang'ın babası × Yang'ın annesi = Yang Meydanı = Yang Mi, Yang Mi, Yang'ın babasının ve Yang'ın annesinin eseridir (ürün, matematiksel bir terim olarak ürün anlamına da gelir), bu nedenle adı "Yang Meydanı "Yang Lifang" a tercih edilir (bu yüzden imzasının "Yang 2" olması gerektiğini öneriyoruz).
Son olarak, bir cümle ile, güç için İngilizce kelime şu şekildedir: p Ower, bu yüzden genellikle p'nin kuvvetine x olarak bir güç fonksiyonu yazarız.
Tamam, şimdi tek vuruşta çizilebilen yaygın Çince karakterlerin sınıflandırmasına geri dönelim. Bunu ilgilenen okuyucular için bir alıştırma olarak bırakıyoruz: Lütfen aşağıdaki 16 Çince karakteri izomorfik ilişkiye göre sınıflandırın: içbükey, dışbükey, bir, ağız, B, Ji, Si, Ji, Çince, Japonca, Japonca, dize, yay, le, Fabrika, zhe.
Belki de Euler'in "topolojik vuruşlar" hakkındaki temel sonuçlarını yayınlamanın zamanı gelmiştir. Burada sadece bir sonuç veriyoruz Ayrıntılı kanıt için lütfen Akademisyen Jiang Boju'nun "Tek Vuruşlu Resim ve Postacı Yolu Problemi" kitabının ilk 28 sayfasına bakın.
Belirli bir ağ için, her köşe için köşelerini işaretleyin, ona bağlı kenarların sayısını sayın ve köşeleri tek ve çift olarak adlandırın. Son olarak, tüm ağın tek köşe noktalarının sayısı M sayılır. aşağıdaki gibi sonuç:
Teorem 1
Teorem 2
Sadece iki not ekliyorum:
İlk olarak, M açıkça izomorfik değişmezdir. Dolayısıyla, "topolojik vuruş sayısı" nın da izomorfik değişmez olduğu çıkarımdır.
İkincisi, Teorem 1'e göre, Eulerin "Königsbergin Yedi Köprüsü" nün aynı anda yürünemeyeceğini kanıtlamak zor değildir; Teorem 2'ye göre, "Königsberg'in Yedi Köprüsü" nün "topolojik vuruşları" 2'dir.
Aslında, genellikle Çince karakterler yazdığımızda, matematikte en basit şekilde tek bir vuruş çizmeye çalışmayız. Bunun nedeni bir alışkanlığımızın (kuralın) olmasıdır: Yazarken yön sırasını soldan sağa ve yukarıdan aşağıya takip edin. . Bu, ağız gibi bir yapının tek bir vuruşuna son verdiğimiz anlamına gelir. Bu, sol üst köşenin nispeten yüksek ve sağ alt köşenin nispeten düşük olduğu konusunda hemfikir olduğumuzu, dolayısıyla su akışının bir döngü oluşturamadığını söylemek gibidir.
Matematiksel olarak, bu, yazdığımızda elde ettiğimiz grafiğin yönlendirilmiş bir grafik olduğunu söylemekle eşdeğerdir. 1736'da Euler'in bir başka temel sonucuna göre, Çince karakterleri yazmak için aşağıdaki kural (kurallar) - başlangıç noktası ve bitiş noktası çakışamayan bağlantılı bir Çince karakter - yönlendirilmiş bir grafiğe sahip bir Çince karakter olarak döngü olmamasını sağlayabilir. Genel yönlendirilmiş bir grafik için, ünlü BEST teoremi (dört matematikçi tarafından B ruijn, van Aardenne ... E hrenfest, S mith, T utte bulundu), döngü sayısını hesaplayabilirsiniz (Euler döngüleri olarak adlandırılır). Bununla birlikte, genel yönsüz grafikler için karşılık gelen bir hesaplama formülü yoktur.
Şimdiye kadar, tanımladığımız şey yalnızca en basit topolojidir ve söz konusu nesne tek boyutludur. Geçen yılki Nobel Ödülü çalışması, yüksek boyutlu grafiklerin topolojik özelliklerini içeriyordu. Umarım yüksek boyutlu grafiklerin topolojisini daha fazla tartışma fırsatımız olur.
Son olarak, bir önizleme olarak, okuyucuya iki boyutlu grafiklerle ilgili bir soru bırakıyoruz (aslında topoloji ile cevaplanabilir).
Düşünce soruları:
Her zamanki temsilinde, iki model olduğunu görebiliriz: biri siyah beşgen, diğeri beyaz altıgen. Soru: Her birinde kaç tane beşgen ve altıgen var? Dahası, küreyi bölmek için beşgen ve altıgen desenlerin kullanımını sınırlarsak (her köşenin kendisine bağlı tam olarak üç kenarı olduğunu varsayarsak); 'dan farklı başka konfigürasyonlar elde edebilir miyiz?

Resim kaynağı: Pixabay
daha fazla okuma :
[1] Akademisyen Jiang Bojunun küçük kitabı "Tek Zamanlı Resim ve Postacı Hat Problemi" nin ikinci yarısı Çinli matematikçi Guan Meigu tarafından önerilen "postacı hattı problemini" tartıştı. Bundan bahsedildiği için bundan yararlanabilecek çok sayıda kurye olmalı Toplam yol uzunluğunun en kısa olması için yürüyüş rotası nasıl düzenlenir.
[2] Grafik teorisinin kimyadaki uygulaması, 1874'te "İzomerlerin matematiksel teorisi" üzerine bir makale yayınlayan İngiliz matematikçi Kelley'ye kadar izlenebilir. Matematiğin kimyada uygulanması için Joseph Malkevitchin Mathematics and Chemistry: Partners in Understanding Our World, adlı inceleme makalesine bakın.
Ouyang Shunxiang, "Matematik Kültürü", Sayı 1, 2016 tarafından çevrilen "Matematik ve Kimya: Dünyanın Yorumunda Bir Çift Ortak" ın Çince çevirisi var.
[3] Daha genel olarak, Nobel Kimya Ödülünde topoloji uygulaması için, Qian Minping'den Jiang Boju'da yer alan Akademisyen Jiang Boju'nun "Topoloji-Topoloji ve Kimyada Kiralite" adlı makalesine bakabilirsiniz. Gong Guanglu, "Matematik Modern Kimya ve Biyolojiye Giriyor", Science Press, 2007.
[4] Grafik teorisi araştırmasının sınırları için, lütfen Profesör Jin Fangrongun bilgi çağında Grafik Teorisi makalesine bakın, AMS Bildirimleri, 57, no. 6, Temmuz 2010, 726-732, notices / 201006 / rtx100600726p.pdf. "Bilgi Çağında Grafik Teorisi" nin Çince çevirisi var,
Teşekkürler
Hong Kong Şehir Üniversitesi'nden Profesör Guanrong Chen ve Chongqing Üniversitesi'nden Profesör Hongliang Shao'ya değerli eleştiri ve önerileri için teşekkür ederiz.